Cassegrain Formulas and Tips by Mike Lockwood
Copyright 2006-2007
A Cassegrain telescope is a bit more complicated to design and build
than a Newtonian. It requires careful placement of the optics in
its setup, and often manipulation of the equations during design.
This discourages some, and annoyed me. It always seemed that I
was going through three different books or
articles to locate the equations I was looking for.
Therefore,
this web page was created to merge the important sources of Cassegrain
formulas that I have come across. I chose some common names for
variables to make things easier to read, since every author seems to
have different variables for the same quantities! I also give a
couple formulas I have derived that show how sensitive the Cassegrain
design is to certain quantities. These are fairly simple to
derive, but I don't see them in the amateur publications that I have.
So, I put them here.
The first part of this page covers general Cassegrain formulae.
All the formulas given here are applicable to all
these types
- classical, Ritchey-Chrétien, Dall-Kirkham.
The
differences
between the various types of Cassegrains are the figures of the primary
and secondary
mirrors,
and they will be covered in the next section, followed by other useful
facts and procedures that I have seen fit to include.
1)
Diagram, Variables,
and Design Formulae
Cassegrain telescopes are built to reduce the physical length of the
telescope tube. By folding the light path and slowing down the
convergence of the light cone, we shorten the tube to about the focal
length of
the primary mirror, while the telescope has a focal length of somewhere
between 3 and 15 times the focal length of the primary! This
allows
high magnification to be obtained from a compact instrument, and it can
reduce some of the mechanical demands cause by having a long tube
structure. However, it requires a second optical surface to be
made and positioned quite accurately, and the whole structure must
maintain the alignment of the mirrors no matter where the telescope is
pointed. The secondary mirror also typically is of significant
size, leading to a central obstruction of between 20% and 40%.
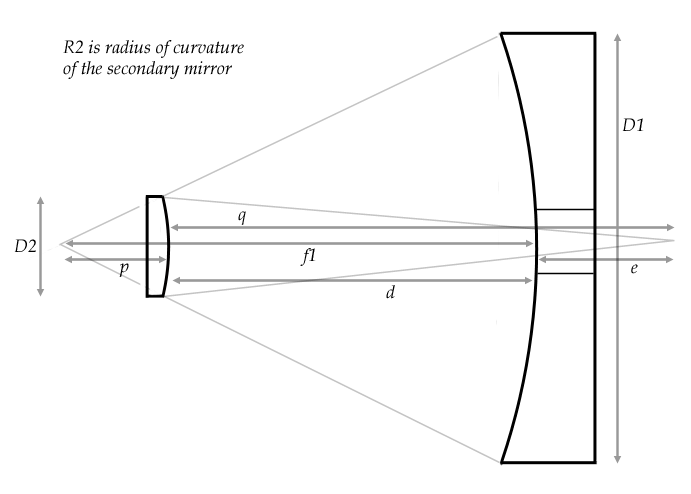
Figure 1:
A diagram of a Cassegrain telescope
is shown above. The distances
between the mirrors and other quantities are illustrated.
The important quantities here are:
the diameters of the primary and secondary mirrors,
D1 and D2,
the focal length of the primary f1,
the primary-secondary separation, d,
the system focal point to secondary distance, q,
the primary mirror surface to focal plane
distance, e, and
the distance from the secondary
surface to the focal point of the primary, p.
The purpose of a Cassegrain secondary mirror is to slow the convergence
of the light cone from the primary (thereby increasing the system focal
length), direct it to the focal plane, and possibly compensate for some
of the image
aberrations caused by the primary. The secondary has a
"magnification factor" that is
referred to as M. This factor tells by how much
the secondary mirror magnifies (or multiplies) the focal length of the
primary by. The overall focal length of the instrument is
designated as F. With that introduction, here are
the important equations for designing a Cassegrain telescope.
They can be manipulated as needed to solve for various
quantities. Most of these equations are from Texereau, another is
from another source.
F = f1*M
(System focal length)
M = q / p
("Magnification" of system)
p = (f1+e)/ (M+1)
(secondary mirror to focal plane distance)
R2 = 2*p*M /
(M -1) (Radius
of
curvature of the secondary mirror)
D2 = D1*p / f1
(Diameter of secondary
required to fully illuminate ONLY the center point of the field.)
s = q / d
(Defined for convenience for later formulas)
Here is a handy equation - how to calculate the radius of curvature of
the secondary if you know p and q. This is
required if you already
have a primary that you wish to use in a Cassegrain. After you
choose
a magnification, you know p and q, and all you
need is the secondary's radius of curvature, R2.
Below is a manipulated form of the equation for R2 given by
Richard Buchroeder from page ~135 of "Advanced Telescope
Making
Techniques, Vol. 1". The first equation is solved for R2. The
second equation is the same relationship solved for q.
R2 = 2 / ((1/p) - (1/q))
q = R2*p / (R2 - 2*p)
The second equation is important because q determines
where the focal plane will be. If we observe that we have q
in terms of both p and R2, we realize
that we can find the sensitivity of the focal plane position as a
function of the location of the secondary and as a function of the
radius of curvature (R2) of the secondary. This
means we can figure out how much moving the
secondary moves the focal plane, and how much an error in the
secondary's
curvature (caused by grinding in a curve that's slightly off) will
affect
the focal plane position. To get these quantities, we simply take
the
derivative of the second equation with respect to p and R2.
Those formulae are given below.
dq / dp = R22
/ (4*p2 - 4*p*R2 +
R22)
dq / dR2 = p/(R2
- 2*p)
- R2*p/(R2 - 2*p)2
For example, for my 12.5" F/12.5 classical Cassegrain, R2
= 47.35", and p = 15.72". Plugging these numbers
into the equation yields dq / dp =
8.86, dq / dR2 = -1.95. These
results are unitless.
The second number means that an error of plus (or minus) one millimeter
in R2
moves the focal plane 1.95mm closer to (or farther from) the secondary
mirror.
The first number means that for every unit of length (say a millimeter)
that the secondary is moved towards the primary mirror, the focal plane
moves 8.86 millimeters farther behind the primary. This
derivative (rate
of change) is only valid for the position of the secondary, and it will
change if the secondary is moved. (The p value
should be recalculated if large moves are anticipated.)
Now, you might wonder why the focal plane moves so much more than we
expect. Common sense seems to indicate that, for the 12.5" F/12.5
Cass, with an F/4.2 primary and a secondary magnification of 12.5/4.2 =
3, moving the secondary 0.01" toward the primary should move the focal
plane back 0.01" * 3 = 0.03". But this is NOT true.
Instead, it moves 0.0886" back. So where does the extra
sensitivity come from? Well, when
you decrease the spacing between the secondary and primary, the focal
length of the system actually gets longer (!), and this adds
dramatically to the sensitivity to spacing changes. This is why
adjusting the spacing between an aspheric secondary and the primary
changes the system correction (see tip a
below).
The sensitivity to changes in these quantities increases as
the magnification rises. For a 14.25" F/21 Cassegrain, dq
/ dp = 31.2, dq / dR2 =
-10.51. As we can see, both quantities rise quite significantly.
So,
that planetary Cassegrain you're thinking about building is going to
require you to design in only a small amount of secondary travel to put
the focal plane exactly where
you want it when you assemble it the first time. Be aware that
the change in length of the tube structure due to temperature will
cause focus shift over the course of a night because that causes the
distance between the primary and secondary mirrors to decrease.
2) Mirror Prescription/Design Formulas
Here I'll give the formulas used to calculate the "prescriptions" of
the primary and secondary mirrors for three types of Cassegrain
telescopes - the
Dall-Kirkham, the classical, and the Ritchey-Chrétien.
(No,
no
Pressmann-Camichels. They're not very useful for astronomy.)
The prescription is the form of the aspheric shape of the
mirror. First, realize that in these designs, the mirrors
require various amounts of aspherization (correction).
Now, you don't really need this next formula, but some of the more
math-oriented ATMs might enjoy seeing it. It was also obtained
from "ATMT Vol 1.",
and I will add the author's name and the page number
soon. A general formula for
the shape of a cross section of a mirror's surface is given by:
z = (y2/R)
/ (1 + [1 - (1+b)(y/R)2]1/2)
(Don't
worry - you don't need this to design your Cassegrain!)
The optical axis lies along the z-axis, and the y-axis
is the transverse axis, so z represents the
mirror's height as a
function of y, the distance off the optical axis.
The center of the mirror is at y
=
0, and its edge is at y = mirror radius. R
is the radius of curvature of the mirror. The variable b
represents the conic constant, which is an important quantity.
For a sphere, b
= 0 (Dall-Kirkham secondary)
For an
ellipse, 0 > b >
-1 (Dall-Kirkham primary)
For a
parabola,
b =
-1 (Newtonian and classical
Cassegrain primary)
For a
hyperbola,
b <
-1 (Ritchey-Chrétien
primary and
secondary, classical Cassegrain secondary)
Basically, the parameter b determines the type of shape
a
concave or convex mirror has. (If b > 0, we
have an oblate spheroid, by
the way.) In order to design a Cassegrain, we
need
to calculate it according to the type of Cassegrain we wish to make.
Thankfully, the formulas are already worked out in Richard
Buchroeder's article mentioned above - he has provided a convenient
table, and I have merely substituted the variables names I have used
here and made simple modifications to them.
|
"Flavor" of Cassegrain
|
b
for primary
mirror
|
b for
secondary
mirror
|
Dall-Kirkham
|
s(M-1)(M+1)2
------------ - 1
M3(M+s)
|
0 (sphere)
|
Classical Cassegrain
|
-1 (parabola)
|
-4M
------ - 1
(M-1)2
|
Ritchey-Chrétien
|
-2s
-----
- 1
M3
|
-4M(M-1)
- 2(M+s)
----------------- - 1
(M-1)3
|
Table I: Equations to determine the conic constant
of primary and secondary mirrors in Cassegrain telescopes
So how to figure the mirrors? Calculate b for the
mirrors in your Cassegrain. For example, in my 12.5" F/12.5
Cassegrain, b = -1 for the primary and b
= -4.00 for the secondary. The primary is a parabola, so we know
how to test that. Since b = -4.00 for the
secondary,
it is a hyperbola with 4.00 times the correction of a
parabola, so if we are to make a concave test plate, we simply multiply
all the ideal knife edge displacements by 4.00. It's that
simple!
Let's say for an R-C primary, b = -1.04167. This
means
that for Foucault testing, we simply multiply the ideal Foucault knife
edge
positions for a parabola by 1.04167, and that gives us the ideal knife
edge positions for the
hyperbolic
primary mirror (or concave test plate for the secondary mirror).
Many are surprised to find out that the primary mirror for an R-C is
only 1.04167 times more corrected than a parabola. The things
that make an R-C difficult are the typically fast focal ratio of the
primary and the significant correction that must be applied to the
secondary mirror.
3) Other Cassegrain Tips
I'm sure this section will get expanded in the future.
a)
Correction issues for Cassegrains with hyperboloidal secondary mirrors
(classical, R-C):
The correction of a Cassegrain
optical system with an aspheric secondary mirror (classical, R-C) is
dependent on the primary-secondary distance. This is because the
secondary's conic constant, b is a function
of how far it is from the
primary mirror and the distance to the focal plane. (This is why
it is difficult to match a secondary mirror that is already finished to
a primary mirror - the chances of the secondary having the right value
of b are
small.) If the secondary has the right conic constant and it is
placed at the proper design location, the system will be perfectly
corrected for spherical aberration. However, if you see spherical
aberration, digest the following:
-If the secondary mirror is moved AWAY
from the primary mirror, the correction of the system will INCREASE.
-If the secondary is moved TOWARD the primary mirror, the correction of
the system will DECREASE. (This assumes it is
large enough to be moved and still intercept all of the light from the
primary)
-If you are figuring a Cassegrain
secondary using star testing, increasing the correction of the
secondary will decrease the correction of the system.
So, if you see a bit of overcorrection in your classical or R-C,
move the secondary mirror closer to the primary and deal with the
focus shift, or figure the secondary to have a bit more
correction. Why is this true? Think about it this way - if
we move the secondary farther from the primary, we use only a smaller,
central portion of the secondary. In effect, the hyperbola in the
center of the secondary has less correction than that of the full
mirror, and this causes the light in the outer zones of the mirror to
converge slightly more slowly, which is the same as increasing the
correction of the whole system. So, the effect on a Cassegrain
system of changing the correction of the secondary mirror is the
OPPOSITE of changing the correction of the primary mirror.
b)
Correction issues
for Dall-Kirkhams:
For Dall-Kirkhams, the position of the (spherical) secondary
makes a
difference, too, as evidenced by the presence of the variables s and M in the
equation for the value of b for the
primary mirror. Those two variables are dependent on q, d and p, which vary
with the location of the secondary mirror. A quick numerical
calculation using the mirror spacings for my 12.5" classical Cassegrain
indicate that if it were a Dall-Kirkham, then moving the secondary
toward the primary would require a
slightly less corrected primary. So,
moving the secondary toward the primary should slightly increase the
correction of a Dall-Kirkham system in the system. This is
the opposite of what happens in the other Cassegrains with
hyperboloidal secondaries. I
believe this system is less sensitive to movement of the secondary than
a classical or R-C. I still need to double-check these results,
though.
c) I
collimate my Nasmyth-focus classical Cassegrain by inserting a laser
collimator and using the following procedure:
- First, I adjust tilt of the focuser to
aim the laser dot at the center of the tertiary mirror, adjusting the
mechanical positions of the tertiary and focuser if necessary, and
making sure that the focuser is square
to the tube. This adjustment should not need to be done very
often.
- Second, I adjust the tertiary's tilt to send the laser dot to the
exact center of the secondary mirror. Before I install the
secondary, I use a permanent marker to draw a ring exactly
centered on the secondary's surface. This makes the tertiary tilt
adjustment (or focuser alignment, for those without a tertiary) much
easier and more accurate.
- Third, I adjust the secondary's tilt to return the laser beam to
the
center of the tertiary and the center of the laser collimator.
- Fourth, and lastly, I remove the laser collimator and put in an
eyepiece. I find a bright
star or planet in the eyepiece. While looking at the star in the
telescope, I adjust the primary's tilt until I remove all of the coma
from the image at the center of the field of view. This takes a
little practice, but once you get the hang of it it is simple, quick,
and very accurate.
This whole procedure can be accomplished in under 5 minutes once it is
understood and practiced. Most of the time is spent on the
primary mirror. There are other techniques (including use of
holographic laser collimators, etc.) that can be used to align the
primary. It should be accepted that critical collimation of a
Cassegrain telescope (especially if the primary mirror is fast) is a
necessity in order for the telescope to function properly. If you
understand this before you build the tube structure, you will avoid
many problems.
d)
Size of illuminated field:
In order for an area of the focal plane to be "fully
illuminated", it must get light from all of the primary and secondary
mirrors. For a Cassegrain this means that the secondary mirror
must be large enough to allow the entire primary mirror to be "seen"
from the parts of the focal plane that we wish to fully
illuminate. For example, if we know the location of the focal
plane and we put our eye there at its center, we should see the
reflection of the primary mirror centered in the secondary
mirror. If only the very center of the field is fully illuminated
(say the central 0.05"), then we should see the reflection of the edge
of the primary mirror right at the edge of the secondary mirror.
If the fully illuminated field is larger, say 0.5" in diameter, then we
should be able to move our eye off the optical axis by 0.25" and still
see the entire primary mirror in the secondary mirror, though it will
no longer be centered in the secondary. (This will soon be
illustrated below.)
More sections will probably be added in the future as I figure out what
information is useful to people.
